ßêàßï ßëñ ßêüßïáßï ßèéßïèßêò ßèòßïÿßï ßî ßèòßêæ

Subtracting A Named Vector From Another Named Vector

Find A Vector A With Representation Given By The Directed Line Segment Aвѓ Bвѓ Draw Aвѓ Bвѓ AndвЂ

Suppose T в в V Suppose S в в V Is Invertible A Prove That T And S вЂ

Operations On Bivectors From Zero To Geo 2 2
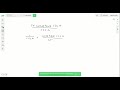
Write Each Expression In Terms Of Sines And Or Cosines And Then Simplify S S1 Cosαtan

A Suppose That Σa N And Σb N Are Series With Positive Terms And Σb N Is C

A Ã Ë Å Y 5 3Ã Ë Å Y 2 B Ã Ë Å A B 3 3Ã Ë Å A B 6Ã Ë Å A B 7
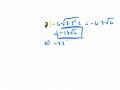
A Ã Ë Å 18 3Ã Ë Å 2 B Ã Ë Å 54 3Ã Ë Å 6 C Ã Ë Å 60x3y3 2xyÃ Ë Å 15
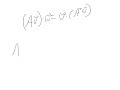
Consider A Finite Sequence Of Vectors S U 1 U 2 U N Let S

Let S Be The Collection Of Vectors X Y In в ќ 2вЂ

Let V Be As In 82 And Let A V V Be A Symmetrie Operator Let λ 1 ł

Show That A Coshi θ Cosθ B Sinhi θ I Sinθ

As Shown

Simplify Each Rational Expression If The Rational Expression Cannot Be Simplified So State S S

Use Basic Logical Equivalences To Show That R Ã Ë Â Ã Â P Ã â â Q Ã Ë Â R Ã Ë Â Ã Â P Ã Ë Â Ã Â Q Is Logicaâ

Prove Theorem 6 2 Let S U 1 U 2 U N Be A Basis For V Over K And Le

If Σa N And Σb N Are Both Divergent Is Σ A N B N Necessarily

The Vector Is Denoted By 0 вџЁ0 0 0 вџ

